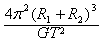问题
选择题
定义在R上的偶函数f(x)满足f(-x)=f(2+x),且在[-1,0]上单调递增,设a=f(3),b=f(
|
答案
由条件f(-x)=f(2+x),可以得:
f(x+2)=f(-x)=f(x),所以f(x)是周期函数.周期为2.
又因为f(x)是偶函数,所以图象在[0,1]上是减函数.
a=f(3)=f(1+2)=f(1),
b=f(
)=f( 1 2
-2)=f(2-1 2
)=f(1 2
)3 2
c=f(2)=f(0)
0<
<13 2
所以c>b>a.
故选D.