阅读下列说明和C++代码,将应填入空 (n) 处的字句写在对应栏内。
[说明]
某饭店在不同的时段提供多种不同的餐饮,其菜单的结构图如图18-27所示。

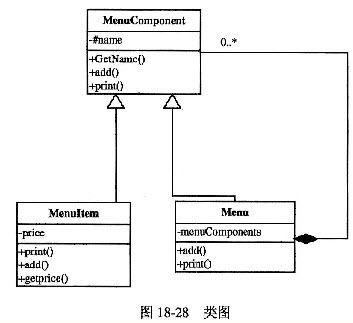
现在采用组合(Composition)模式来构造该饭店的菜单,使得饭店可以方便地在其中增加新的餐饮形式,得到如图18-28所示的类图。其中MenuComponent为抽象类,定义了添加(add)新菜单和打印饭店所有菜单信息(print)的方法接口。类Menu表示饭店提供的每种餐饮形式的菜单,如煎饼屋菜单、咖啡屋菜单等。每种菜单中都可以添加子菜单,例如图18-27中的甜点菜单。类MenuItem表示菜单中的菜式。
[C++代码]
#include<iostream>
#include<list>
#Include<string>
using namespace std;
class MenuComponent
protected:string name;
public:
MenuComponent(String name)(this->name=name;
string getName()return name;
(1) ; //添加新菜单
virtual void print()=0; //打印菜单信息
;
class Menultem:public MenuComponent
private:double price;
public:
Menultem(string name,double price):MenuComponent(name)(this->price=price;
double getPrice()return price;
void add(MenuComponent *menuComponent)retum;//添加新菜单
void print()cout<<" "<<getName0<<","<<getPrice0<<end1;
;
class Menu:public MenuC0mponent
private:list< (2) >menuComponents;
public:
Menu(string name):MenuComponent(name)
void add(MenuComponent *menuComponent)//添加新菜单
(2) ;
VOid print()
cout<<"\n"<<getNameO<<"\n---------------"<<end1;
Std::list<MenuComponent*>::iterator iter,
for(iter=menuComponents.begin0;iter!=menuComponents.end0;iter++)
(4) ->print();
;
void main()
MenuComponent *al IMenus=new Menu("ALL MENUS");
MenuComponent *dinerMenu=new Menu("DINER MENU");
……∥创建更多的Menu对象,此处代码省略
alIMenus->add(dinerMenu); ∥将dinerMenu添加到餐厅菜单中
……∥为餐厅增加更多的菜单,此处代码省略
(5) ->printO; ∥打印饭店所有菜单的信息
(1)处填()。