问题
解答题
已知:关于x的方程①x2﹣(m+2)x+m﹣2=0有两个符号不同的实数根x1,x2,且x1>|x2|>0;关于x的方程②mx2+(n﹣2)x+m2﹣3=0有两个有理数根且两根之积等于2.求整数n的值.
答案
解:由方程①知:∵x1x2<0,x1>|x2|>0,
∴x1>0,x2<0,
∵△=(m﹣2)2+8>0,
∴x1+x2=m+2>0,x1x2=m﹣2<0,
∴﹣2<m<2,
由方程②知: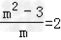 ,
,
∴m2﹣2m﹣3=0,
∴m=3(舍去),m=﹣1
代入②得:x2﹣(n﹣2)x+2=0,
∵方程的两根为有理数,
∴△=(n﹣2)2+8=k2,
∴△=(n﹣2)2﹣k2=﹣8,(n﹣2+k)(n﹣2﹣k)=﹣8,
∴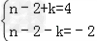 或
或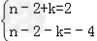 ,
,
∴n=3或n=1.
