问题
选择题
函数f（x）是定义在R上的奇函数，当x∈（0，+∞）时，f（x）=lg（x+1），那么当x∈（-∞，0）时，f（x）的解析式是（ ）
A．y=-lg（1-x）
B．y=lg（1-x）
C．y=-lg|x+1|
D．y=-lg（x+1）
答案
设x＜0，则-x＞0，
因为当x∈（0，+∞）时，f（x）=lg（x+1），
所以f（-x）=lg（-x+1）．
因为函数f（x）是定义在R上的奇函数，
所以f（-x）=-f（x），所以f（x）=-lg（-x+1）．
故选A．
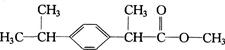关于有机物X的说法中，错误的是