问题
问答题
设函数f(u)在(0，+∞)内具有二阶导数，且z=f(
)满足等式
若f(1)=0，f’(1)=1，求函数f(u)的表达式．
答案
参考答案：中的方程改写成
uf"(u)+f’(u)=0，即 [uf’(u)]’=0
积分得 uf’(u)=C1．
由f’(1)=1，得C1=1，从而有f’(u)=
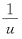，再次积分得f(u)=lnu+C．
又由f(1)=0，得C=0，从而有f(u)=lnu，u＞0．