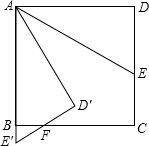
如图，∵正方形ABCD的边长为

3

，∠DAE=30°，

∴DE=AD•tan30°=

3

×

3

3

=1，

AE=2DE=2，

∵∠BAE=∠BAD-∠DAE=90°-30°=60°，旋转角为60°，

∴旋转后AE′在直线AB上，

∴BE′=AE′-AB=2-

3

，

设D′E′与BC相交于F，

∵∠E′=∠AED=90°-30°=60°，

∴BF=BE′•tan60°=（2-

3

）×

3

=2

3

-3，

∴△AD′E′与四边形ABCE重叠部分的面积=S_△AD′E′-S_△BE′F=

1

2

×

3

×1-

1

2

×（2-

3

）×（2

3

-3），

=

3

2

-

7 3

2

+6，

=6-3

3

．

故答案为：6-3

3

．