问题
解答题
定义在R上的奇函数f(x),当x∈(0,1)时,f(x)=
(1)求函数f(x)在(-1,1)的解析式; (2)判断函数f(x)在(-1,0)上的单调性并证明. |
答案
(1)当x∈(-1,0)时,-x∈(0,1).
∵f(x)是奇函数,∴f(x)=-f(-x)=-
=-2-x 4-x+1 2x 4x+1
由f(0)=f(-0)=-f(0),
且f(1)=-f(-1)=-f(-1+2)=-f(1),
得f(0)=f(1)=f(-1)=0.
∴在区间[-1,1]上,有f(x)=
x∈(0,1)2x 4x+1 -
x∈(-1,0)2x 4x+1 0 x∈{-1,0,1}
(2)f(x)在(0,1)上单调递减.
证明当x∈(-1,0)时,f(x)=
,设-1<x1<x2<0,2x 4x+1
则f(x1)-f(x2)=
-2x1 4x1+1
=2x2 4x2+1 (2x2-2x1)(2x1+x2-1) (4x1+1)(4x2+1)
∵-1<x1<x2<0,,∴2x2-2x1>0,2x2+x1-1<0,∴f(x1)-f(x2)>0,即f(x1)>f(x2),故f(x)在(0,1)上单调递减.

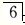 大面积银汞合金充填,远中食物嵌塞,要求固定修复。
大面积银汞合金充填,远中食物嵌塞,要求固定修复。