问题
选择题
已知函数f(x)对任意实数x均有f(-x)=-f(x),f(π-x)=f(x)成立,当x∈[0,
|
答案
当
≤x≤ 2π时,0≤2π-x≤3π 2 π 2
∵f(-x)=-f(x),f(π-x)=f(x)
∴f(2π-x)=f[π-(x-π)]=f(x-π)=-f(π-x)=-f(x)
而当x∈[0,
]时,f(x)=cosx-1π 2
则f(2π-x)=cos(2π-x)-1=cosx-1=-f(x)
∴f(x)=-cosx+1
故选D.

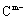 、
、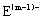 具有相同的电子层结构;③A与B在同一周期,在该周期所有主族元素中,A的原子半径最大,B的离子半径最小;④A与B质子数之和是D质子数的3倍。依据上述信息用相应的化学用语回答下列问题:
具有相同的电子层结构;③A与B在同一周期,在该周期所有主族元素中,A的原子半径最大,B的离子半径最小;④A与B质子数之和是D质子数的3倍。依据上述信息用相应的化学用语回答下列问题: