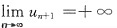参考答案：D

解析： 由题意可知，函数f(x)在(0，+∞)上具有二阶导数，并且f^"(x)＞0，所以可以判断函数f(x)在(0，+∞)是凹函数．由于f^"(x)＞0，因此f^’(x)是单调递增函数，f(x)有以下几种情形，用图示法进行选择：
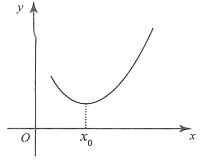
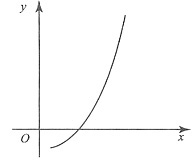
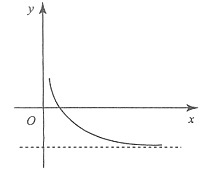
当u₁=f(1)＞u₂=f(2)时，这时，f(n)=u_n的变化有三种可能：
第一种，所示：

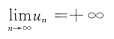
第二种，所示：

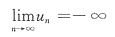
第三种，所示：

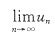存在．
因此否定了A、B．
当u₁＜u₂时只有如图2的可能，即

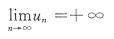．选D．
下面再对正确选项D进行证明：
由拉格朗日中值定理，有
u_n+1-u_n=f(n+1)-f(n)
=f^’ (ξ_n)(n+-n)=f^’(ξ_n)，
其中 ξ_n∈(n，n+1)，n=1，2，…，
由于f^"(x)＞0，那么f^’(x)单调递增，
故 f’(ξ₁)＜f’(ξ₂)＜…＜f’(ξ_n)＜…，
所以　　　　

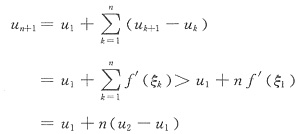
于是当u₂-u₁＞0时，可以得出