问题
选择题
已知函数f(x)是定义在[a-1,2a]上的偶函数,且当x>0时,f(x)单调递增,则关于x的不等式f(x-1)>f(a)的解集为( )
|
答案
因为f(x)是定义在[a-1,2a]上的偶函数,
所以(a-1)+2a=0,解得a=
.1 3
则f(x)定义域为[-
,2 3
].2 3
由偶函数性质知,f(x-1)>f(a)可化为f(|x-1|)>f(
),1 3
又x>0时,f(x)单调递增,所以|x-1|>
①,1 3
又-
≤x-1≤2 3
②,2 3
联立①②解得
≤x<1 3
或2 3
<x≤4 3
,5 3
故不等式f(x-1)>f(a)的解集为[
,1 3
)∪(2 3
,4 3
].5 3
故选C.

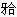 ,家族无类似畸形。有咬上唇习惯。上前牙略舌倾,下前牙直立,可退至切
,家族无类似畸形。有咬上唇习惯。上前牙略舌倾,下前牙直立,可退至切