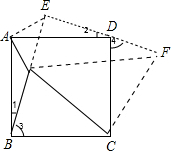
四边形ABCD为正方形，PA=1，PB=2，PC=3，

把△PAB绕A点逆时针旋转90°得△EAD，把△CPB绕C点顺时针旋转90°得△CFD，连PE，PF，如图，

∴∠1=∠2，∠3=∠4，

而∠1+∠3=90°，

∴∠2+∠4=90°，

而∠ADC=90°，

∴∠EDF=180°，即E，D，F共线；

由旋转的性质得到△APE，△CPF均为等腰直角三角形，并且ED=PB=2，DF=PB=2，

∴S_△APE=

1

2

×1×1=

1

2

；S_△CPF=

1

2

×3×3=

9

2

，

在△PEF中，PE=

2

，PF=3

2

，EF=4，

∴PF²=PE²+EF²，

∴△PEF为直角三角形，∠PEF=90°，

∴S_△PEF=

1

2

×EP×EF=

1

2

×

2

×4=2

2

，

∴S_{正方形ABCD}=S_{五边形APCFE}=S_△PEF+S_△APE+S_△CPF=2

2

+5．

故答案为2

2

+5．