问题
选择题
已知椭圆C:
|
答案
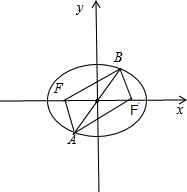
如图所示,
在△AFB中,|AB|=10,|BF|=8,cos∠ABF=
,4 5
由余弦定理得
|AF|2=|AB|2+|BF|2-2|AB||BF|cos∠ABF
=100+64-2×10×8×4 5
=36,
∴|AF|=6,∠BFA=90°,
设F′为椭圆的右焦点,连接BF′,AF′.
根据对称性可得四边形AFBF′是矩形.
∴|BF′|=6,|FF′|=10.
∴2a=8+6,2c=10,解得a=7,c=5.
∴e=
=c a
.5 7
故选B.