如图(a)所示,在光滑绝缘水平面的AB区域内存在水平向右的电场,电场强度E随时间的变化如图(b)所示.不带电的绝缘小球P2静止在O点.t=0时,带正电的小球P1以速度v0从A点进入AB区域,随后与P2发生正碰后反弹,反弹速度大小是碰前的倍,P1的质量为m1,带电量为q,P2的质量m2=5m1,A、O间距为L0,O、B间距L=.已知=,T=.
(1)求碰撞后小球P1向左运动的最大距离及所需时间.
(2)讨论两球能否在OB区间内再次发生碰撞.
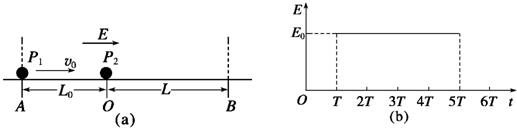
(1)P1经t1时间与P2碰撞,则t1=
P1、P2碰撞,设碰后P2速度为v2,由动量守恒:m1v0=m1(-v0)+m2v2
解得v1=v0(水平向左) v2=(水平向右)
碰撞后小球P1向左运动的最大距离:Sm=又:a1==
解得:Sm=
所需时间:t2==
(2)设P1、P2碰撞后又经△t时间在OB区间内再次发生碰撞,且P1受电场力不变,由运动学公式,以水平向右为正:S1=S2则:-v1△t+a1△t2=v2△t
解得:△t==3T(故P1受电场力不变)
对P2分析:S2=v2△t=v0•=L0<L=
所以假设成立,两球能在OB区间内再次发生碰撞.
答:(1)碰撞后小球P1向左运动的最大距离为,所需时间为.
(2)两球能在OB区间内再次发生碰撞.


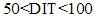 时,经济运行处于()。
时,经济运行处于()。