问题
解答题
已知数列{an}满足8an+1=an2+m(n,m∈N*),且a1=1.
(1)求证:当m=12时,1≤an<an+1<2;
(2)若an<4对任意的n≥1(n∈N)恒成立,求m的最大值.
答案
证明:(1)①当n=1时,a1=1,又8a2=12+a12,a2=
,13 8
∴1=a1<a2<2.
②假设n=k时,1≤ak<ak+1<2成立,
当n=k+1时,有8ak+2=12+ak+12<12+22=16,
∴ak+2<2成立,
由假设ak2<ak+12有8(ak+2-ak+1)=ak+12-ak2>0,
∴ak+2>ak+1≥ak≥1,
∴1≤ak+1<ak+2<2.
故由①,②知,对任意n∈N*都有1≤an<an+1<2成立.
(2)由于an+1-an=
+m 8
(1 8
-8an)=a 2n
(an-4)2+1 8
≥m-16 8
,an≥a1+(n-1)m-16 8
=1+m-16 8
(n-1),m-16 8
①当m>16时,显然不可能使an<4对任意n∈N*成立,
②当m≤16时,an<4对任意n∈N*有可能成立,
当m=16时,a1<4,
假设ak<4,由8ak+1=16+ak2<16+42,ak+1<4.
所以m=16时,对任意n∈N*都有an<4成立,
所以m≤16时,an<4,
故m的最大值是16.

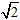 sin100πt (V)的 正弦交流电源,图中电流表内阻不计.副线圈接入“110V,60W”灯泡一只,且灯光正常发光.下列说法正确的是( )
sin100πt (V)的 正弦交流电源,图中电流表内阻不计.副线圈接入“110V,60W”灯泡一只,且灯光正常发光.下列说法正确的是( ) /22 A
/22 A