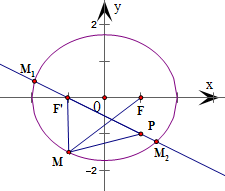
设F'为椭圆的左焦点，连结MF'，作过P、F'的直线交椭圆于

M₁、M₂两点，如图所示

∵

x2

4

+

y2

3

=1中，a=2，b=

3

，

∴c=

a2-b2

=1，可得F（1，0），F'（-1，0）．

由椭圆的定义，得|MF|+|MF'|=2a=4，

∴|MP|+|MF|=|MP|+（4-|MF'|）=4+（|MP|-|MF'|）

由平面几何知识，得-|PF'|≤|MP|-|MF'|≤|PF'|，

∴当M与M₁重合时，|MP|-|MF'|达到最大值|PF'|；当M与M₂重合时，|MP|-|MF'|达到最小值-|PF'|．

由|PF'|=

(1+1)2+(-1-0)2

=

5

，可得|MP|-|MF'|的最大值为

5

，最小值为-

5

．

∴|MP|+|MF|=4+（|MP|-|MF'|）的取值范围为[4-

5

，4+

5

]．

故答案为：[4-

5

，4+

5

]．