问题
选择题
设F1、F2分别为椭圆C:
|
答案
连接MF2,则ON是△MF1F2的中位线,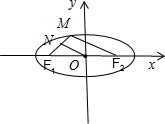
∴|NF1|+|NO|=
(|MF1|+|MF2|)=a,1 2
又∵∠MF1O=
,|OF1|=c,且ON⊥MF1,π 3
∴|NF1|=
c,|NO|=1 2
c,3 2
∴
c+1 2
c=a,3 2
解得e=
=c a
=2 1+ 3
-1.3
故选:A.
设F1、F2分别为椭圆C:
|
连接MF2,则ON是△MF1F2的中位线,
∴|NF1|+|NO|=
(|MF1|+|MF2|)=a,1 2
又∵∠MF1O=
,|OF1|=c,且ON⊥MF1,π 3
∴|NF1|=
c,|NO|=1 2
c,3 2
∴
c+1 2
c=a,3 2
解得e=
=c a
=2 1+ 3
-1.3
故选:A.