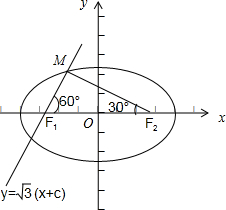
∵椭圆的方程为

x2

a2

+

y2

b2

=1（a＞b＞0），作图如右图：

∵椭圆的焦距为2c，

∴直线y=

3

（x+c）经过椭圆的左焦点F₁（-c，0），又直线y=

3

（x+c）与椭圆交于M点，

∴倾斜角∠MF₁F₂=60°，又∠MF₁F₂=2∠MF₂F₁，

∴∠MF₂F₁=30°，

∴∠F₁MF₂=90°．

设|MF₁|=x，则|MF₂|=

3

x，|F₁F₂|=2c=2x，故x=c．

∴|MF₁|+|MF₂|=（

3

+1）x=（

3

+1）c，

又|MF₁|+|MF₂|=2a，

∴2a=（

3

+1）c，

∴该椭圆的离心率e=

c

a

=

2

3 +1

=

3

-1．

故选：B．