设椭圆的方程为

x2

a2

+

y2

b2

=1（a＞b＞0），F、F'分别是椭圆的左右焦点，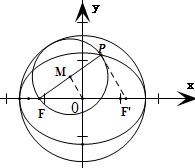

作出以线段PF为直径的圆和以长轴为直径的圆x²+y²=a²，如图所示．

设PF中点为M，连结PF'，

∴OM是△PFF'的中位线，可得|OM|=

1

2

|PF'|，即两圆的圆心距为

1

2

|PF'|

根据椭圆定义，可得|PF|+|PF'|=2a，

∴圆心距|OM|=

1

2

|PF'|=

1

2

（2a-|PF|）=a-

1

2

|PF|，

即两圆的圆心距等于它们半径之差，

因此，以PF为直径的圆与以长半轴为直径的圆x²+y²=a²相内切．

故选：B