问题
填空题
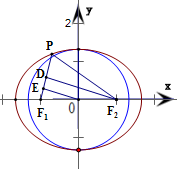
设F1,F2是椭圆
|
答案
∵点P在椭圆C上,∴根据椭圆的定义,可得|PF1|+|PF2|=2a.
又∵|PF2|=|F1F2|=2c,∴|PF1|=2a-2c
过点F2作F2D⊥PF1于D点,过点O作OE⊥PF1于E点,
∵|PF2|=|F1F2|,
∴△PF1F2是等腰三角形,可得D是PF1的中点,DF1=
|PF1|=a-c,1 2
Rt△DF1F2中,|DF1|2+|DF2|2=|F1F2|2,
∴|DF2|=
=|F1F2|2-|DF1|2
=4c2-(a-c)2
.3c2+2ac-a2
∵△DF1F2中,OE是中位线,∴|OE|=
|DF2|=1 2 1 2
.3c2+2ac-a2
又∵以原点O为圆心,以b为半径的圆与直线PF1有公共点,
∴原点O到直线PF1的距离小于b,即|OE|≤b,得1 2
≤b,3c2+2ac-a2
化简得3c2+2ac-a2≤4(a2-c2),即7c2+2ac-5a2≤0,两边都除以a2得7e2+2e-5≤0,解之得-1≤e≤
.5 7
结合椭圆的离心率e∈(0,1),可得0<e≤
.5 7
又∵等腰△PF1F2中,|PF2|+|F1F2|>|PF2|,
∴2c+2c>2a-2c,得a<3c,所以e=
>c a
.1 3
综上所述,椭圆的离心率e的取值范围是(
,1 3
].5 7
故答案为:(
,1 3
]5 7