问题
填空题
已知椭圆
|
答案
∵椭圆
+x2 16
=1的左、右焦点分别为F1、F2，y2 9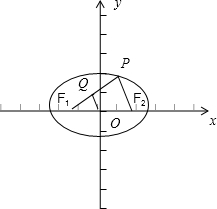 
P是椭圆上的一点，
∴设|PF1|=x，则|PF2|=8-x，
∵Q是PF1的中点，
∴OQ是△PF1F2的中位线，
∵|OQ|=1，
∴8-x=2，
解得x=6．
即|PF2|=6．
故答案为：6．
搜题请搜索小程序“爱下问搜题”
已知椭圆
|
∵椭圆
+x2 16
=1的左、右焦点分别为F1、F2，y2 9
P是椭圆上的一点，
∴设|PF1|=x，则|PF2|=8-x，
∵Q是PF1的中点，
∴OQ是△PF1F2的中位线，
∵|OQ|=1，
∴8-x=2，
解得x=6．
即|PF2|=6．
故答案为：6．
