问题
问答题
如图所示，相邻两车站间距相等，在一条直线上. 车在两站间行驶时平均速度均为v车，每次靠站停顿时间均为t. 某同学位于车站1与车站2之间离车站2较近的某一位置，当车从车站3开动的同时，他向车站2以平均速度v人奔跑，并恰能在汽车离站前赶上汽车，车长不计. 于是该同学得出结论：若他仍以此平均速度从原位置向车站1奔跑，也一定能赶得上这辆班车.
|
答案
当人离车站2的距离x≥S/3时就能赶上车
结论不正确，能不能赶上车与初始位置有关。（2分） 设人离车站2的距离为x，1到2,2到3车站之间的距离为S，由题义人到车站2赶上车则有，
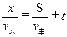（4分）① 如人从该处向1车站跑又有，
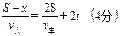②
解①②两式得x="S/3" (2分) 所以当人离车站2的距离x≥S/3时就能赶上车。