(1) 数列{a_n}是首项为a₁=99,公差d=-2的等差数列.

(2) 数列{b_n}的前n项和为S_n′=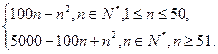

(1)a_n=S_n-S_n-1=(100n-n²)-［100·(n-1)-(n-1)²］=101-2n(n≥2).

∵a₁=S₁=100×1-1²=99=101-2×1,

∴数列{a_n}的通项公式为a_n=101-2n(n∈N^*).

又a_n+1-a_n=-2为常数,∴数列{a_n}是首项为a₁=99,公差d=-2的等差数列.

(2)令a_n=101-2n≥0,得n≤50.5.

∵n∈N^*,∴n≤50(n∈N^*).

①当1≤n≤50时,a_n>0,此时b_n=|a_n|=a_n,所以{b_n}的前n项和S_n′=100n-n².

②当n≥51时,a_n<0,此时b_n=|a_n|=-a_n,

由b₅₁+b₅₂+…+b_n=-(a₅₁+a₅₂+…+a_n)=-(S_n-S₅₀)=S₅₀-S_n,

得数列{b_n}的前n项和为

S_n′=S₅₀+(S₅₀-S_n)=2S₅₀-S_n=2×2 500-(100n-n²)="5" 000-100n+n².

由①②得数列{b_n}的前n项和为S_n′=