问题
解答题
等差数列{an}中,a1<0,S9=S12,该数列前多少项的和最小?
答案
该数列前10项或前11项的和最小
由条件S9=S12可得
9a1+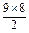 d=12a1+
d=12a1+ d,即d=-
d,即d=-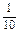 a1.
a1.
由a1<0知d>0,即数列{an}为递增数列.
方法一 由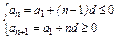 ,
,
得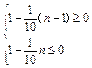 ,解得10≤n≤11.
,解得10≤n≤11.
∴当n为10或11时,Sn取最小值,
∴该数列前10项或前11项的和最小.
方法二 ∵S9=S12,∴a10+a11+a12=3a11=0,∴a11=0.
又∵a1<0,∴公差d>0,从而前10项或前11项和最小.
方法三 ∵S9=S12,
∴Sn的图象所在抛物线的对称轴为x=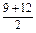 =10.5,
=10.5,
又n∈N*,a1<0,∴{an}的前10项或前11项和最小.
方法四 由Sn=na1+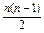 d=
d=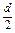
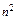 +
+ n,
n,
结合d=-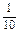 a1得
a1得
Sn=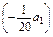 ·n2+
·n2+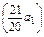 ·n
·n
=-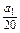
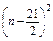 +
+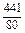 a1(a1<0),
a1(a1<0),
由二次函数的性质可知n=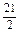 =10.5时,Sn最小.
=10.5时,Sn最小.
又n∈N*,故n=10或11时Sn取得最小值.
