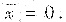问题
问答题
设有摆线
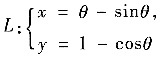(-π≤θ≤π)，试求：
(Ⅰ)L绕x轴旋转一周所得旋转面的面积；
(Ⅱ)L与x轴所围平面图形的形心
.
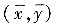答案
参考答案：(Ⅰ)这是由参数方程给出的曲线. 由于
x′(θ)=1-cosθ，y′(θ)=sinθ，
则按旋转面面积计算公式，可得该旋转面的面积
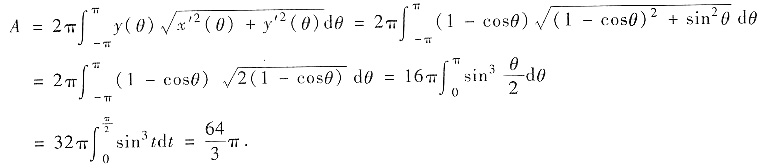
(Ⅱ)由平面图形的形心公式，有
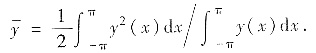
当x=θ-sinθ时θ∈[-π，π]对应θ∈[-π，π]，相应地y(x)=1-cosθ
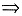
因此
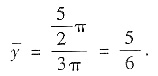
由对称性知，
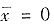. 故所求平面图形的质心为
.
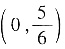解析：本题有如下变式：
(Ⅰ)求L的弧长l.
解：按弧长计算公式：
(Ⅱ)求L上任意点的曲率.
解：按参数式求导法，先求出
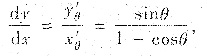
再求出
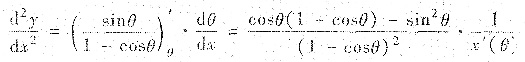
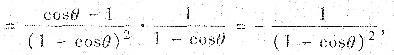
最后按曲率公式，L上
点处的曲率为
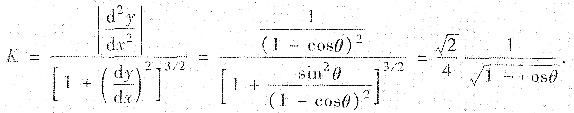
(Ⅲ)求曲线型物体L的形心
解：按形心公式得
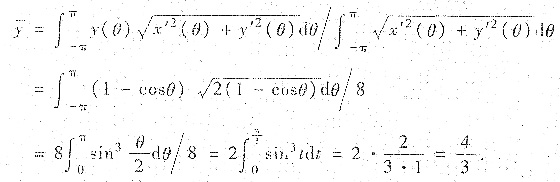
由对称性同样得
