设x>y,试比较代数式-(8-10x)与-(8-10y)的大小,如果较大的代数式为正数,则其中最小的正整数x或y的值是多少?
解:由两式作差得-(8-10x)-[-(8-10y)]=-8+10x+8-10y=10x-10y。
因为x>y,所以10x>10y,即10x-10y>0。
所以-(8-10x)>-(8-10y)。
又由题意得-(8-10x)>0,即x>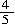 ,所以x最小的正整数值为1。
,所以x最小的正整数值为1。
设x>y,试比较代数式-(8-10x)与-(8-10y)的大小,如果较大的代数式为正数,则其中最小的正整数x或y的值是多少?
解:由两式作差得-(8-10x)-[-(8-10y)]=-8+10x+8-10y=10x-10y。
因为x>y,所以10x>10y,即10x-10y>0。
所以-(8-10x)>-(8-10y)。
又由题意得-(8-10x)>0,即x>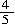 ,所以x最小的正整数值为1。
,所以x最小的正整数值为1。