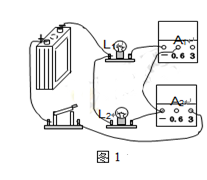
问题
填空题
点P在椭圆
|
答案
∵椭圆
+x2 4
=1中,c2=4-3=1,y2 3 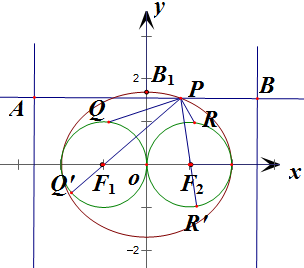
∴椭圆
+x2 4
=1两焦点F1(-1,0),F2(1,0),y2 3
恰为两圆(x+1)2+y2=1和(x-1)2+y2=1的圆心,
在椭圆
+x2 4
=1中,e=y2 3
,准线x=±4,1 2
过P点作x轴平行线,分别交两准线于A,B两点,
连接PF1,PF2,并延长,
分别交两圆于Q′,R′,
则|PQ|+|PR|≤|PQ′|+|PR′|
=|PF1|+1+|PF2|+1
=e|PA|+e|PB|+2
=e|AB|+2
=
×8+21 2
=6.
故答案为:6.