求空间曲线积分
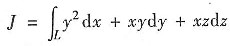 ,其中L是圆柱面x2+y2=2y与平面y=z-1的交
,其中L是圆柱面x2+y2=2y与平面y=z-1的交
线,从x轴正向看去取逆时针方向.
参考答案:[分析与求解一] L的方程是
 L的参数方程是
L的参数方程是
z=cost,y=1+sint,z=2+sint.
按L的定向t从0到2π,于是代公式得
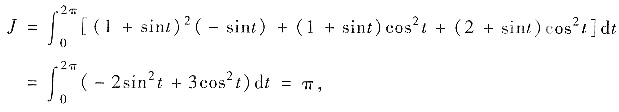
其中

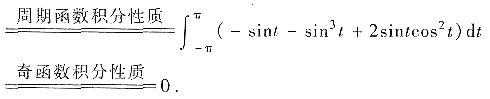
[分析与求解二] L是空间中的平面曲线,可用斯托克斯公式转化为求平面上的曲面积分,圆柱面所截平面y=z-1部分记为∑,按右手法则取上侧,用斯托克斯公式,将曲线积分,化为∑上的第二类曲面积分,有
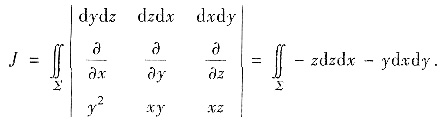
∑在xy平面的投影区域易求,即Dxy:x2+(y-1)2≤1.
将此曲面积分J投影到xy平面化为二重积分,则
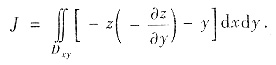
∑的方程为


[分析与求解三] L是母线平行于z轴的柱面与平面的交线,可投影到xy平面上,然后用格林公式.
由L的方程
 z=y+1,dz=dy,L在xy平面上的投影曲线记为Γ:x2+(y-1)2=1,z=0. 相应地也取逆时针方向,于是代入积分表达式得
z=y+1,dz=dy,L在xy平面上的投影曲线记为Γ:x2+(y-1)2=1,z=0. 相应地也取逆时针方向,于是代入积分表达式得

其中Dxy是Γ所围的圆域.
解析:①在[分析与求解二]中,斯托克斯公式也可用第一类曲面积分表示,即

由∑的方程y=z-1及∑的法向量朝上可知,∑的方向余弦

其中σ是∑的面积,它在xy平面上的投影面积是
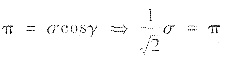
 J=π
J=π
②当空间曲线L的参数方程易写出且被积表达式又较简单时可考虑直接代公式化为定积分来计算空阅曲线积分,计算定积分时要注意利用周期函数与奇偶函数的积分性质来简化计算.
③当空间曲线是平面曲线或特殊的曲面(如球面)上的曲线时,常可考虑用斯托克斯公式将空间曲线积分化为平面或特殊曲面(如球面)上的面积分,以简化计算
④当空间曲线L是以Oxy平面曲线l为准线,母线平行于z轴的柱面与曲面z=f(x,y)的交线时,它们的定向相同,求

可投影到xy平面,转化为求平面曲线积分
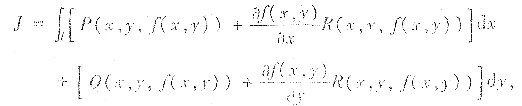
就是将z=f(x,y)代入被积表达式,其中
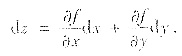
本题的[分析与求解三]就是用的这种方法.
