∵椭圆

x2

a2

+

y2

b2

=1中，c=

a2-b2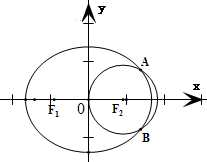

，

∴椭圆的焦点为F₁（-c，0）和F₂（c，0）．

由此可得圆（x-c）²+y=c²的圆心为F₂（c，0），半径r=c．

∵圆（x-c）²+y=c²与椭圆恰有两个公共点，

∴椭圆的右顶点（a，0）在圆的内部，

可得（a-c）²+0²=c²，解之得a＜2c，

因此椭圆的离心率e=

c

a

＞

1

2

，结合e∈（0，1），可得

1

2

＜e＜1．

故答案为：

1

2

＜e＜1