（1）∵a_n+1=2S_n,∴S_n+1-S_n=2S_n,∴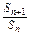=3.

又∵S₁=a₁=1,

∴数列{S_n}是首项为1、公比为3的等比数列，

S_n=3^n-1(n∈N^*).

当n≥2时，a_n=2S_n-1=2·3^n-2(n≥2),

∴a_n=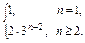

（2）T_n=a₁+2a₂+3a₃+…+na_n.

当n=1时，T₁=1;

当n≥2时，T_n=1+4·3⁰+6·3¹+…+2n·3^n-2,                            ①

3T_n=3+4·3¹+6·3²+…+2n·3^n-1,                                   ②

①-②得：

-2T_n=-2+4+2(3¹+3²+…+3^n-2)-2n·3^n-1

=2+2·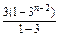-2n·3^n-1

=-1+(1-2n)·3^n-1.

∴T_n=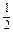+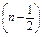·3^n-1(n≥2).

又∵T₁=a₁=1也满足上式，

∴T_n=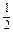+3^n-1(n-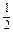) (n∈N^*).