证明略

a₁=S₁=p+q

当n≥2时，a_n=S_n－S_n－1=p^n－1(p－1)

∵p≠0,p≠1,∴=p

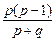若{a_n}为等比数列，则=p

∴=p,

∵p≠0，∴p－1=p+q，∴q=－1

这是{a_n}为等比数列的必要条件.

下面证明q=－1是{a_n}为等比数列的充分条件

当q=－1时，∴S_n=pⁿ－1(p≠0,p≠1)，a₁=S₁=p－1

当n≥2时，a_n=S_n－S_n－1=pⁿ－p^n－1=p^n－1(p－1)

∴a_n=(p－1)p^n－1  (p≠0,p≠1)

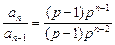=p为常数

∴q=－1时，数列{a_n}为等比数列即数列{a_n}是等比数列的充要条件为q=－1.