问题
选择题
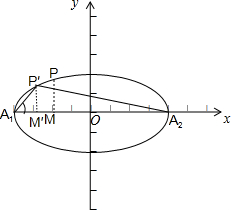
已知A1,A2为椭圆
|
答案
当∠P′A1A2=45°时,直线A1P′的方程为y=x+2,
与椭圆的方程
+y2=1联立,x2 4
,y=x+2
+y2=1x2 4
消去y得:5x2+16x+12=0,即(x+2)(5x+6)=0,
解得x=-
或x=-2(舍去).6 5
∴当∠P′A1A2=45°时,点P′在x轴上的射影M′的坐标为(-
,0),6 5
∴|A1M′|=|-
+2|=6 5
,4 5
∴|A2M′|=|A1A2|-|A1M′|=4-
=4 5
,16 5
显然,当点M在x轴从点M′向右移动到A2的过程中,椭圆上的对应点P从点P′移动到A2,总满足∠PA1A2<45°,
∴满足∠PA1A2<45°的概率为P(M)=
=|M′A2| |A1A2|
=16 5 4
.4 5
故选:A.
