问题
解答题
已知{an}是等差数列,a1=2,a2=3,若在每相邻两项之间插入3个数,使它和原数列的数构成一个新的等差数列,
(1)原数列的第12项是新数列的第几项?
(2)新数列的第29项是原数列的第几项?
答案
(1)原数列的第12项是新数列的第45项.
(2)新数列的第29项是原数列的第8项.
数列的通项公式是研究数列问题的重要工具.能否由条件找到两个数列的通项公式是解决此题的关键.
∵数列{an}中a1=2,d=a2-a1=3-2=1,
∴an=a1+(n-1)d=2+(n-1)×1=n+1.
设新数列为{bn},公差为d′,据题意知b1=2,b5=3,
则d′=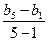
=
=
,
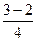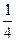∴bn=2+(n-1)×=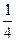
+
.
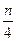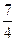(1)a12=12+1=13,令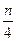+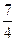=13,得n=45,故原数列的第12项是新数列的第45项.
(2)b29=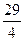
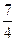+=9,令n+1=9,得n=8,故新数列的第29项是原数列的第8项.