由题意，设边PF₁的中点为Q，连接F₂Q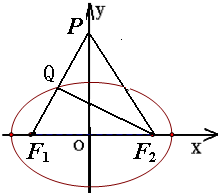

在△QF₁F₂中，∠QF₁F₂=60°，∠QF₂F₁=30°

Rt△QF₁F₂中，|F₁F₂|=2c（椭圆的焦距），

∴|QF₁|=

1

2

|F₁F₂|=c，|QF₂|=

3

2

|F₁F₂|=

3

c

根据椭圆的定义，得2a=|QF₁|+|QF₂|=（1+

3

）c

∴椭圆的离心率为e=

c

a

=

2c

(1+ 3 )c

=

3

-1

故选：A