问题
解答题
已知函数f（x）=2x-2-x，数列{an}满足f（log2an）=-2n.
（1）求数列{an}的通项公式；
（2）求证：数列{an}是递减数列.
答案
（1）an=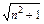
-n（2）证明见解析
（1）解 ∵f（x）=2x-2-x，
∴f（log2an）=2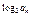
-2
=-2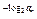n，
即an-
=-2n.∴a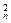
+2n·an-1=0.
∴an=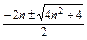
，又an＞0，∴a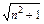n=-n.
（2）证明 ∵an＞0，且an=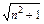-n,
∴
=
=
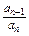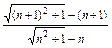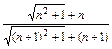＜1.
∴an+1＜an.即{an}为递减数列.