问题
解答题
已知一个凸四边形ABCD的四边的长顺次为a、b、c、d，且a2+ab-ac-bc=0，b2+bc-bd-cd=0，试判断这个四边形是否是中心对称图形。
答案
解：∵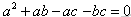
∴
∴
∵
∴
∴
∴
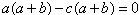
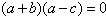
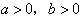
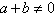
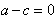
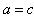
同理由b2+bc-bd-cd=0，可知b=d
∴可知四边形ABCD是平行四边形，所以这个四边形是中心对称图形。
搜题请搜索小程序“爱下问搜题”
已知一个凸四边形ABCD的四边的长顺次为a、b、c、d，且a2+ab-ac-bc=0，b2+bc-bd-cd=0，试判断这个四边形是否是中心对称图形。
解：∵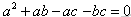
∴
∴
∵
∴
∴
∴
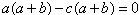
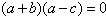
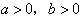
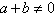
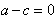
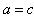
同理由b2+bc-bd-cd=0，可知b=d
∴可知四边形ABCD是平行四边形，所以这个四边形是中心对称图形。