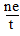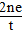椭圆x29+y25=1的左、右焦点分别为F1，F2，弦AB过F1，若△ABF2的

问题填空题

椭圆

=1的左、右焦点分别为F₁，F₂，弦AB过F₁，若△ABF₂的内切圆周长为2π，A，B两点的坐标分别为（x₁，y₁）和（x₂，y₂），则|y₂-y₁|的值为______．

答案

椭圆：

=1，a=3，b=

，∴c=2，左、右焦点F₁（-2，0）、F2（2，0），△ABF2的内切圆周长为2π，则内切圆的半径为r=1，

而△ABF₂的面积=△AF₁F₂的面积+△BF₁F₂的面积=

×|y₁|×|F₁F₂|+

×|y₂|×|F₁F₂|=

×（|y₁|+|y₂|）×|F₁F₂|=2|y₂-y₁|（A、B在x轴的上下两侧）

又△ABF₂的面积═

×|r（|AB|+|BF₂|+|F₂A|=

×1×（2a+2a）=2a=6．

所以 2|y₂-y₁|=6，|y₂-y₁|=3．

故答案为3．