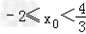问题
解答题
已知动点P与双曲线2x2﹣2y2=1的两个焦点F1,F2的距离之和为4.
(1)求动点P的轨迹C的方程;
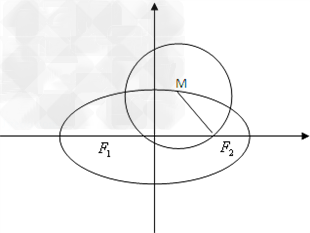
(2)若M为曲线C上的动点,以M为圆心,MF2为半径做圆M.若圆M与y轴有两个交点,求点M横坐标的取值范围.
答案
解:(1)双曲线2x2﹣2y2=1的两个焦点F1(﹣1,0),F2(1,0),
∵|PF1|+|PF2|=4>|F1F2|,
∴P点的轨迹是椭圆,其中a=2,c=1,则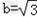 ,
,
∴C的方程为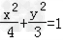
(2)设M(x0,y0),d=|x0|,
∵圆M与y轴有两个交点,
∴d<r,即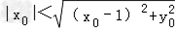 ,
,
∴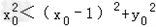 ,
,
又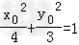 ,即
,即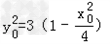 ,
,
∴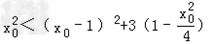 ,
,
∴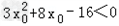 ,
,
∴(3x0﹣4)(x0+4)<0
∴ ,
,
又﹣2≤x0≤2,
∴