问题
选择题
已知函数f(x)为奇函数,x>0时为增函数且f(2)=0,则{x|f(x-2)>0}=( )
A.{x|0<x<2或x>4}
B.{x|x<0或x>4}
C.{x|x<0或x>6}
D.{x|x<-2或x>2}
答案
由于函数f(x)为奇函数,x>0时为增函数且f(2)=0,
可得函数在(-∞,0)上单调递增,且f(-2)=0,
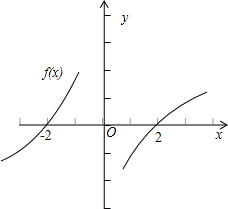
故函数f(x)的单调性示意图如图所示:
由函数的图象可得-2<x-2<2,或-2x-2<0,
解得 0<x<2或x>4,
故选:A.