问题
选择题
设{an}递增等差数列,前三项的和为12,前三项的积为48,则它的首项是( )
A.1
B.2
C.4
D.6
答案
答案:B
本题考查等差数列通项公式和基本运算.
设公差为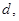 则
则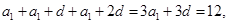 即
即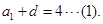 又
又
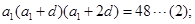 又(1),(2)得
又(1),(2)得 即
即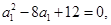 解得
解得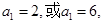 因为数列是递增等差数列,
因为数列是递增等差数列,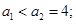 所以
所以 故选B
故选B
设{an}递增等差数列,前三项的和为12,前三项的积为48,则它的首项是( )
A.1
B.2
C.4
D.6
答案:B
本题考查等差数列通项公式和基本运算.
设公差为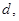 则
则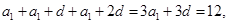 即
即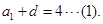 又
又
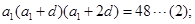 又(1),(2)得
又(1),(2)得 即
即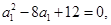 解得
解得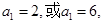 因为数列是递增等差数列,
因为数列是递增等差数列,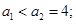 所以
所以 故选B
故选B