问题
选择题
已知椭圆
|
答案
∵椭圆方程为
+x2 25
=1,y2 9
∴椭圆的a=5,长轴2a=10,可得椭圆上任意一点到两个焦点F1、F2距离之和等于10.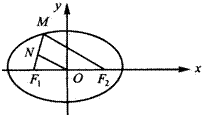
∴|MF1|+|MF2|=10
∵点M到左焦点F1的距离为2,即|MF1|=2,
∴|MF2|=10-2=8,
∵△MF1F2中,N、O分别是MF1、F1F2中点
∴|ON|=
|MF2|=4.1 2
故选D.
已知椭圆
|
∵椭圆方程为
+x2 25
=1,y2 9
∴椭圆的a=5,长轴2a=10,可得椭圆上任意一点到两个焦点F1、F2距离之和等于10.
∴|MF1|+|MF2|=10
∵点M到左焦点F1的距离为2,即|MF1|=2,
∴|MF2|=10-2=8,
∵△MF1F2中,N、O分别是MF1、F1F2中点
∴|ON|=
|MF2|=4.1 2
故选D.