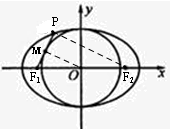
设以椭圆的短轴为直径的圆与线段PF₁相切于点M，连结OM、PF₂，

∵M、O分别为PF₁、F₁F₂的中点，

∴MO∥PF₂，且|PF₂|=2|MO|=2b，

又∵线段PF₁与圆O相切于点M，可得OM⊥PF₁，

∴PF₁⊥PF₂，

Rt△PF₁F₂中，|F₁F₂|=2c，|PF₂|=2b，

∴|PF₁|=

|F1F2|2-|PF2|2

=

4c2-4b2

，

根据椭圆的定义，得|PF₁|+|PF₂|=2a，

∴

4c2-4b2

+2b=2a，即

c2-b2

=a-b，

两边平方得：c²-b²=（a-b）²，即a²-2b²=（a-b）²，化简得2ab-3b²=0，解得b=

2

3

a，

因此，c=

a2-b2

=

5

3

a，可得椭圆的离心率e=

c

a

=

5

3

．

故选：A