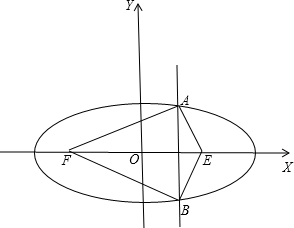
设椭圆的右焦点为E．如图：

由椭圆的定义得：△FAB的周长：AB+AF+BF=AB+（2a-AE）+（2a-BE）=4a+AB-AE-BE；

∵AE+BE≥AB；

∴AB-AE-BE≤0，当AB过点E时取等号；

∴AB+AF+BF=4a+AB-AE-BE≤4a；

即直线x=m过椭圆的右焦点E时△FAB的周长最大；

此时△FAB的高为：EF=2．

此时直线x=m=c=1；

把x=1代入椭圆

x2

4

+

y2

3

=1的方程得：y=±

3

2

．

∴AB=3．

所以：△FAB的面积等于：S_△FAB=

1

2

×3×EF=

1

2

×3×2=3．

故答案为：3．