问题
解答题
已知一椭圆经过点(2,-3),且与椭圆9x2+4y2=36有共同的焦点,
(1)求椭圆方程;
(2)若P为椭圆上一点,P、F1、F2是一个直角三角形的顶点,且|PF1|>|PF2|,求|PF1|:|PF2|的值.
答案
解:(1)∵9x2+4y2=36,
∴a=3,b=2,c=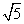 ,
,
与之有共同焦点的椭圆可设为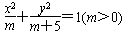 ,
,
代入(2,-3)点,解得m=10或m=-2(舍),
故所求方程为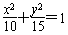 ;
;
(2)①若∠PF2F1=90°,则|PF2|=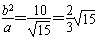 ,
,
∴|PF1|=2a-|PF2|=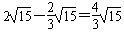 ,
,
于是|PF1|:|PF2|=2;
②若∠F1PF2=90°,则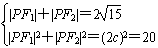 ,
,
令|PF1|=p,|PF2|=q,
得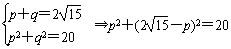 ,
,
∵Δ<0,∴无解,即这样的三角形不存在;
综合①②知|PF1|:|PF2|=2。
