问题
填空题
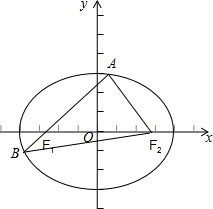
过椭圆
|
答案
∵椭圆的方程为
| x2 |
| 16 |
| y2 |
| 9 |
∴a=4，b=3，又过焦点F1的直线与椭圆交于A，B两点，A，B与椭圆的另一个焦点F2构成△ABF2，
则△ABF2的周长l=|AB|+|AF2|+|BF2|=（|AF1|+|AF2|）+（|BF1|+|BF2|）=2a+2a=4a=16．
故答案为：16．
搜题请搜索小程序“爱下问搜题”
过椭圆
|
∵椭圆的方程为
| x2 |
| 16 |
| y2 |
| 9 |
∴a=4，b=3，又过焦点F1的直线与椭圆交于A，B两点，A，B与椭圆的另一个焦点F2构成△ABF2，
则△ABF2的周长l=|AB|+|AF2|+|BF2|=（|AF1|+|AF2|）+（|BF1|+|BF2|）=2a+2a=4a=16．
故答案为：16．
阅读图片，回答问题。
 | |
| 图一指南针 |  |
| 图二麦哲伦船队远洋航船 |