问题
解答题
已知P为曲线E上的任意一点，F1（﹣1，0），F2（1，0），且|PF1|+|PF2|=2|F1F2|．
（1）求曲线E的方程；
（2）若点P在第二象限，∠F2F1P=120°，求△F2F1P的面积．
答案
解：（1）∵F1（﹣1，0），F2（1，0），
∴|PF1|+|PF2|=2|F1F2|=4．
因此，曲线E表示以F1、F2为焦点，长轴2a=4的椭圆，c=1，b2=a2﹣c2=3
∴曲线E的方程为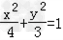
（2）∵△F2F1P中，∠F2F1P=120°，F1F2=2
∴根据余弦定理，得|F1F2|2=|PF1|2+|PF2|2﹣2|PF1||PF2|cos120°=4，
化简得|PF1|2+|PF2|2+|PF1||PF2|=4…①
又∵|PF1|+|PF2|=4，可得|PF1|2+|PF2|2+2|PF1||PF2|=16…②
∴②减①，得|PF1||PF2|=12
根据正弦定理，可得△F2F1P的面积S=
|PF1||PF2|sin120°=3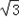
．