问题
解答题
已知椭圆C的中心在坐标原点，焦点在x轴上，椭圆C上的点到焦点距离的最大值为3，最小值为1。
（1）求椭圆C的标准方程；
（2）若直线l：y=kx+m与椭圆C相交于A，B两点（A，B不是左右顶点），且以AB 为直径的圆过椭圆C的右顶点，求证：直线l过定点，并求出该定点的坐标。
答案
解：（1）由题意设椭圆的标准方程为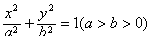
由已知得a+c=3，a-c=1，
∴a=2，c=1，
∴b2=a2-c2=3
∴椭圆的标准方程为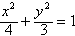
。
（2）设A（x1，y1），B（x2，y2），联立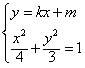
得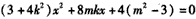
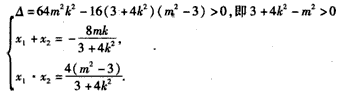
又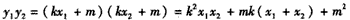
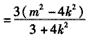
因为以AB为直径的圆过椭圆的右顶点D（2，0）
∴
∴
∴
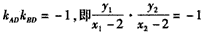
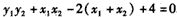
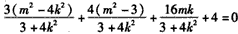
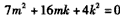
解得m1=-2k，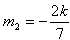
且均满足3+4k2-m2>0
当m1=-2k时，l的方程为y=k（x-2），直线过定点（2，0），与已知矛盾；
当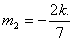
时，l的方程为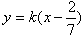
直线过定点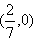
所以，直线l过定点，定点坐标为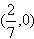
。