问题
填空题
已知{an}为等差数列，且a7－2a4＝－1，a3＝0，则公差d＝ ．
答案
－
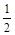
解：设等差数列{an}的首项为a1，公差为d，由等差数列的通项公式以及已知条件得
a1+6d-2(a1+3d)="-1"
a1+2d=0 ，
即 a1="1" a1+2d=0 ，
解得d=-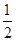
搜题请搜索小程序“爱下问搜题”
已知{an}为等差数列，且a7－2a4＝－1，a3＝0，则公差d＝ ．
－
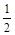
解：设等差数列{an}的首项为a1，公差为d，由等差数列的通项公式以及已知条件得
a1+6d-2(a1+3d)="-1"
a1+2d=0 ，
即 a1="1" a1+2d=0 ，
解得d=-