问题
解答题
某书店正在销售某种课外读本,进价12元/本,售价20元/本,为了促销,书店决定凡是买10本以上的班级,每多买一本,售价就降价0.10元(例如,某班买20本这种课外 读本,于是每本降价0.10×(20 - 10)=1元,就可以按 19元/本的价格购买),但是最低价为16元/本。
(1)求一个班一次至少买多少本,才能以最低价购买?
(2)写出当一次购买x本时(x>10),利润y(元)与购买量x (本)之间的函数关系式;
(3)有一天,某校九年级(1)班买了46本,九年级(2)班买了50本,书店发现卖50本比卖46本赚的钱少,为了使每次多 卖多赚,在其他促销条件不变的情况下,最低价16元/本,至少要提高到多少?请说明理由。
答案
解:(1)设买x本,由题意得20-0.1,(x-10)≤16,
解得x≥50;
(2)由题意得
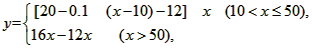
即y=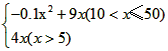
(3)由y=-0.1x2+9x
即y=-0.1(x-45)2+202.5知
当10<x≤45时,y随x的增大而减小,
∴要使多卖多赚,当x>45时,价格不能低于20-0.10× (45-10)=16.5(元),
故最低价格16元/本至少要提高到16.5元/本。
