已知f（x）是定义在实数集上的奇函数，且当x＞0时，f（x）=2x．

问题解答题

已知f（x）是定义在实数集上的奇函数，且当x＞0时，f（x）=2^x．

（1）当x＜0时，求f（x）的解析式；

（2）画出函数f（x）的图象；

（3）写出函数f（x）的单调区间．

答案

（1）若x＜0，则-x＞0，

∵当x＞0时，f（x）=2^x．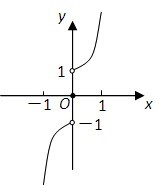

∴f（-x）=2^-x．

∵f（x）是定义在实数集上的奇函数，

∴f（-x）=-f（x），

即f（-x）=2^-x=-f（x），

∴f（x）=-2^-x，x＜0．

（2）由（1）知f（x）=

2x，x＞0

0，x=0

-2-x，x＜0

，作出函数的图象如图：

（3）由图象可知，函数的单调增区间为（-∞，+∞）．