问题
解答题
已知函数f(x)=x+
(1)用函数单调定义研究函数f(x)在区间(0,+∞)上的单调性; (2)判断函数f(x)的奇偶性,并证明之; (3)根据函数的单调性和奇偶性作出函数f(x)的图象,写出该函数的单调减区间. |
答案
(1)任意取x1,x2∈(0,+∞)且x1<x2.f(x1)-f(x2)=(x1+
)-(x2+3 x1
)=(x1-x2)(1-3 x2
)=(x1-x2)3 x1x2
(3分)x1x2-3 x1x2
因为x1<x2所以x1-x2<0
当x1,x2∈(0,
]时,0<x1x2<3所以x1x2-3<03
所以f(x1)-f(x2)>0即f(x1)>f(x2).
所以f(x)在(0,
]上是单调减函数.(6分)3
同理可证f(x)在(
,+∞)上是单调增函数.(8分)3
(2)函数f(x)的定义域为x|x≠0,x∈R关于原点对称(9分)
因为f(-x)=-x-
=-f(x).3 x
所以f(x)是奇函数.(12分)
(3)图象为
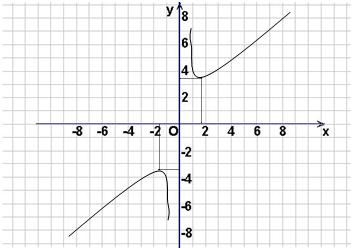 (14分)
(14分)
函数f(x)的单调减区间为(-
,0)和(0,3
)(16分)3

